JOURNAL DES SCIENCES MILITAIRES.
Janvier 1883.

LA CRYPTOGRAPHIE MILITAIRE.

« La cryptographie est un auxiliaire puissant de la tactique militaire. » (Général Lewal, Études de guerre.)

I. LA CRYPTOGRAPHIE DANS L’ARMÉE

A. Notions historiques.

La Cryptographie ou l’Art de chiffrer est une science vieille comme le monde ; confondue à son origine avec la télégraphie militaire, elle a été cultivée, dès la plus haute antiquité, par les Chinois, les Perses, les Carthaginois ; elle a été enseignée dans les écoles tactiques de la Grèce, et tenue en haute estime par les plus illustres généraux romains [1].

Depuis la modeste scytale des Lacédémoniens et les trucs inventés ou rapportés par Æneas-le-Tacticien [2], jusqu’au fameux tonneau de Kessler [3], les hommes de guerre ont imaginé bien des procédés pour transmettre au loin des ordres secrets, ou pour mettre leurs instructions à l’abri des investigations et des surprises de l’ennemi.

Nous ne possédons cependant que des renseignements fort incomplets sur les procédés cryptographiques proprement dits en usage chez les anciens ; en dehors des Commentaires d’Ænéas, on ne rencontre au sujet de la question qui nous occupe, que des passages isolés dans Polybe [4], Plutarque [5], Dion Cassius [6], Suétone [7], Aulu-Gelle [8], Isidore [9] et Jules l’Africain [10].

Pendant le Moyen-Age, la cryptographie n’a guère été cultivée que par les moines et les cabalistes, et encore, là où elle a servi à un but pratique quelconque, les inventeurs ont-ils plutôt cherché à donner le change sur le sens des communications transmises, qu’à imaginer des méthodes de correspondance plus ou moins indéchiffrables ; c’est qu’en ces temps d’ignorance ombrageuse, il était tout aussi dangereux de correspondre dans un langage mystérieux ou indéchiffrable, que d’écrire en clair les secrets les plus compromettants.

Même au xvii^e siècle, le simple fait d’avoir correspondu en caractères secrets était encore considéré comme circonstance aggravante par les tribunaux anglais ; ainsi dans le fameux procès intenté au comte de Sommerset, pour crime d’empoisonnement, le chancelier Bacon releva, comme une charge grave contre le noble accusé, son habitude d’écrire en chiffres à ses amis.

C’était donc de la stéganographie que pratiquaient nos pères, artificium sine secreti latentis suspicione scribendi, plutôt que de la cryptographie, dans le sens que nous attachons aujourd’hui à ce mot. On peut lire dans les œuvres du jésuite Schott [11] et dans un vieux traité de cryptographie du duc de Brunswick [12], les mille artifices qu’ils ont successivement inventés. Ce n’est qu’à partir de la Renaissance que la cryptographie devient un art véritable, ars occulte scribendi, comme on disait, et qu’elle acquiert une certaine importance dans les correspondances des princes avec leurs ambassadeurs, et dans les relations des grands seigneurs avec leurs affidés.

On a vu, par ses lettres adressées au landgrave de Hesse, publiées il y a quelques années par de Rommal, que Henri IV aimait à se servir d’un chiffre pour sa correspondance intime.

On sait également que Henri IV ayant fait intercepter quelques lettres chiffrées adressées par des membres de la Ligue au gouvernement espagnol, chargea le mathématicien Viète d’en trouver la clef. Celui-ci y réussit, et le roi put ainsi, pendant près de deux ans, surveiller les intrigues de ses ennemis.

Sous Richelieu, l’art de déchiffrer les écritures secrètes s’éleva presque à la hauteur d’une science d’État ; au dire du maréchal de camp Beausobre [13], le ministre des affaires étrangères avait même une académie où elle était enseignée [14]. Soutenu par les largesses des gouvernants, encouragé par l’absence de probité politique qui caractérise les règnes suivants, l’art de déchiffrer a continué, jusqu’à la révolution de Juillet, d’être cultivé avec un égal succès par les espions de la cour et les hommes du cabinet noir.

Je n’ai pu cependant trouver des traces bien nettes de l’emploi de la correspondance cryptographique dans l’armée, au xvi^e siècle ; mais on sait positivement que, dès le xviii^e siècle, les ordres ne se transmettaient aux généraux commandant sur les frontières ou en pays ennemi, que par chiffres [15].

Dans les récits des guerres du premier Empire, il est souvent question de communications cryptographiques ; les généraux avaient deux clefs pour correspondre entre eux et avec l’état-major général : le grand chiffre et le petit ou chiffre banal. Le baron Fain, le secrétaire de Napoléon I^er, rapporte que pendant la guerre de Russie l’Empereur entretenait des correspondances chiffrées [16]. On sait également que, pendant la guerre d’Espagne, un Espagnol trouva moyen de dérober le chiffre de Suchet, et s’en servit pour faciliter à ses compatriotes la reprise de Mequinenza et de Lerida.

Aujourd’hui, la correspondance par chiffres secrets est adoptée dans toutes les armées de l’Europe; mais elle n’est encore appliquée d’une façon systématique que dans les bureaux des chancelleries.

B. État de la question.

Les Allemands posent en principe que la correspondance cryptographique doit être employée de la manière la plus étendue ; les programmes de leurs écoles militaires prescrivent non seulement d’exercer les officiers à la composition et à la lecture des dépêches secrètes, mais encore de les initier à la connaissance de tous les principes théoriques de l’art de déchiffrer.

L’article 32 du règlement du 19 janvier 1874 porte également que les dépêches militaires doivent, autant que possible, être chiffrées.

On pourrait donc s’étonner au premier abord que, à de rares exceptions près, l’usage de la correspondance chiffrée soit encore limité aujourd’hui, dans l’armée française, aux commandants en chef. Mais un système de cryptographie « d’un emploi facile et sûr est une lacune, » dit le général Lewal, « qui a toujours existé dans notre armée [17]. » L’ancien commandant de l’École supérieure de guerre ajoute, il est vrai, qu’il existe bien des procédés à cet effet, et qu’il suffirait d’en adopter un « qui fût à la fois portatif et d’un usage à la portée de tous ; » mais certaines déceptions, éprouvées par l’état-major dans notre récente campagne de Tunisie, aussi bien que les méthodes enseignées et préconisées dans nos hautes écoles militaires, ne feraient-elles pas supposer qu’il existe une singulière analogie entre ce système facile et sûr et la pierre philosophale des anciens chimistes ?

Nos meilleurs généraux sont bien d’avis, aujourd’hui, qu’il est indispensable que les différents commandants d’une armée aient à leur disposition un système de communications secrètes pour correspondre librement, non seulement entre eux et avec leur commandant en chef, mais encore avec leurs lieutenants ; ainsi, le tacticien que je viens de citer pense qu’il faudrait pourvoir d’un chiffre en temps de paix comme en temps de guerre, les généraux, les chefs de régiment ou de service, tous les commandants de colonne et de poste. Il ajoute même, et avec raison, qu’il faudrait, durant la paix, exercer nos officiers au maniement de cette correspondance.

« C’est une affaire à prévoir et à régler avant la guerre, dit-il ; « une fois les opérations commencées il est trop tard pour y songer. D’ailleurs, même en paix, on a besoin, et à chaque instant, de correspondre secrètement. »

On lit dans les Recherches historiques sur l’art militaire du général Bardin [18] que l’usage des chiffres s’était éteint au milieu de la conflagration de 1814, et que, lorsque Napoléon voulut réunir au noyau de l’armée toutes ses garnisons de l’étranger et plusieurs grandes garnisons françaises, ce fut en pur et clair français que Feltre et Berthier expédièrent ses ordres ; aussi, peu de dépêches parvinrent à destination, l’ennemi s’empara de la plupart. « Peut-être, dit Bardin, le sort de la France et la face de l’Europe ont-ils dépendu de la désuétude de la cryptographie ! »

Mais il ne suffit pas d’avoir un chiffre de correspondance secrète, il faut encore qu’il présente des garanties sérieuses d’indéchiffrabilité ; or, c’est le côté faible de la plupart des systèmes imaginés jusqu’à ce jour, et là où ce défaut capital a été écarté, on se trouve en présence d’inconvénients pratiques tout aussi graves. Même au ministère de la guerre on ne s’est pas montré très heureux jusqu’ici dans le choix ou la combinaison du chiffre. Ce n’est un secret pour personne que pendant la guerre turco-russe on reçut, un dimanche, d’un des attachés militaires qui suivaient les opérations des armées en lutte, une dépêche chiffrée qui, par suite de l’absence du chef de bureau chargé de la correspondance cryptographique, ne put être déchiffrée. Le Ministre, qui ignorait la clef de la dépêche, ne crut alors pouvoir mieux faire que de prier un des officiers de l’état-major d’en essayer le déchiffrement sans clef : au bout de quelques heures le cryptogramme était traduit ! Heureusement pour le secret de la correspondance, l’habile déchiffreur était le fils du Ministre lui-même [19].

On a pu voir par les articles nécrologiques publiés en 1879 dans les journaux allemands, à l’occasion de la mort du capitaine Max Hering, le chef du service télégraphique, qui découvrit en 1870 le câble de la Seine, quels services a rendus aux assiégeants l’absence d’un système sûr de correspondance secrète entre l’armée de Paris et les généraux de la province.

Je ne sais ce qu’il faut penser des affirmations des journalistes d’outre-Rhin ; mais lorsque je vois des juges autorisés déclarer que la cryptographie est un « auxiliaire puissant de la tactique militaire, » et que je songe que les destinées d’un pays, le sort d’une ville ou d’une armée, pourraient à l’occasion dépendre de la plus ou moins grande indéchiffrabilité d’un cryptogramme, je suis stupéfait de voir nos savants et nos professeurs enseigner et recommander pour les usages de la guerre des systèmes dont un déchiffreur tant soit peu expérimenté trouverait certainement la clef en moins d’une heure de temps.

On ne peut guère s’expliquer cet excès de confiance dans certains chiffres que par l’abandon dans lequel la suppression des cabinets noirs et la sécurité des relations postales ont fait tomber les études cryptographiques ; il est également permis de croire que les affirmations peu mesurées de certains auteurs, non moins que l’absence complète de tout travail sérieux sur l’art de déchiffrer les écritures secrètes, ont largement contribué à donner cours aux idées les plus erronées sur la valeur de nos systèmes de cryptographie.

C’est ainsi que le général Lewal affirme catégoriquement dans ses Études de guerre [20] que les chiffres à base variable sont illisibles, ou du moins qu’on n’arrive à les déchiffrer qu’avec des difficultés inouies ! Et Voltaire lui-même n’a-t-il pas dit dans un article consacré aux écritures chiffrées, et cela à l’époque où l’art de déchiffrer était dans toute sa floraison, que « ceux qui se « vantent de déchiffrer une lettre sans être instruits des affaires « qu’on y traite, et sans avoir de secours préliminaires, sont de « plus grands charlatans que ceux qui se vanteraient d’entendre « une langue qu’ils n’ont point apprise [21] »

Dans la préface du Contr’espion, [22] où « le citoyen » Dlandol faisait connaître, en 1793, les clefs de quelques chiffres dont se servaient les royalistes dans leurs correspondances avec les émigrés, il est dit que « ce n’était pas un des moindres services à rendre à la patrie dans les circonstances d’alors que d’anéantir par la publicité l’arme la plus dangereuse des ennemis secrets de la République ». Je crois, à mon tour, ne pas faire acte de mauvais citoyen en mettant au grand jour un état de choses qui,  pour relever d’un ordre d’idées différent, n’en est pas moins identique au fond, et dont nos ennemis du dehors ne pourraient un jour que trop bien et trop aisément tirer parti.

Dans les pages qui suivent, j’examinerai d’abord les desiderata de tout système de cryptographie militaire ; puis je dirai quelques mots sur les différents chiffres ; j’indiquerai ensuite un nouveau procédé de déchiffrement applicable aux systèmes de cryptographie à base variable les plus usités ; je finirai par quelques considérations sur les dictionnaires chiffrés et les cryptographes ^4[23].

II. DESIDERATA DE LA CRYPTOGRAPHIE MILITAIRE.

Il faut bien distinguer entre un système d’écriture chiffrée, imaginé pour un échange momentané de lettres entre quelques personnes isolées, et une méthode de cryptographie destinée à régler pour un temps illimité la correspondance des différents chefs d’armée entre eux. Ceux-ci, en effet, ne peuvent, à leur gré et à un moment donné, modifier leurs conventions ; de plus, ils ne doivent jamais garder sur eux aucun objet ou écrit qui soit de nature à éclairer l’ennemi sur le sens des dépêches secrètes qui pourraient tomber entre ses mains.

Un grand nombre de combinaisons ingénieuses peuvent répondre au but qu’on veut atteindre dans le premier cas ; dans le second, il faut un système remplissant certaines conditions exceptionnelles, conditions que je résumerai sous les six chefs suivants :

1. Le système doit être matériellement, sinon mathématiquement, indéchiffrable ;

2. Il faut qu’il n’exige pas le secret, et qu’il puisse sans inconvénient tomber entre les mains de l’ennemi ;

3. La clef doit pouvoir en être communiquée et retenue sans le secours de notes écrites, et être changée ou modifiée au gré des correspondants ;

4. Il faut qu’il soit applicable à la correspondance télégraphique ;

5. Il faut qu’il soit portatif, et que son maniement ou son fonctionnement n’exige pas le concours de plusieurs personnes ;

6. Enfin, il est nécessaire, vu les circonstances qui en commandent l’application, que le système soit d’un usage facile, ne demandant ni tension d’esprit, ni la connaissance d’une longue série de règles à observer.

Tout le monde est d’accord pour admettre la raison d’être des trois derniers desiderata ; on ne l’est plus, lorsqu’il s’agit des trois premiers.

C’est ainsi que des personnes autorisées soutiennent que l’indéchiffrabilité absolue du chiffre ne saurait être considérée comme une condition sine quâ non de son admission dans le service de l’armée ; que les instructions chiffrées transmises en temps de guerre n’ont qu’une importance momentanée, et n’exigent guère le secret au delà des trois ou quatre heures qui suivent le moment où elles ont été données ; qu’il importe donc peu que le sens d’une dépêche secrète soit connu de l’ennemi quelques heures après son interception ; qu’il suffit, en un mot, que le système soit combiné de telle façon que la traduction d’un cryptogramme exige au moins trois à quatre heures de travail. On ajoute que la possibilité de pouvoir changer de clef à volonté ôte d’ailleurs au défaut de non-indéchiffrabilité toute son importance.

Cette argumentation peut, au premier abord, paraître assez juste ; au fond, je la crois fausse.

C’est en effet, selon moi, oublier que le secret des communications envoyées à distance conserve très souvent son importance au delà de la journée où elles ont été transmises ; sans énumérer toutes les éventualités qui peuvent se présenter, il me suffira de citer le cas où le commandant d’une ville assiégée envoie des renseignements à l’armée qui doit la secourir. De plus, une fois qu’un cryptogramme intercepté a pu être déchiffré, toute nouvelle dépêche, écrite avec la même clef et qui subit le même sort, peut être lue instantanément. Il arrivera par suite que, pendant un temps plus ou moins long, des dépêches seront expédiées dans toutes les directions, dont le déchiffrement se trouvera en quelque sorte fait d’avance : à moins d’admettre que dans un corps d’armée toutes les instructions chiffrées émanent d’un seul, ou du moins passent par les mains d’un seul, ce qui serait réduire la correspondance secrète à un rôle singulièrement modeste.

La faculté de pouvoir changer de clef à volonté est certainement une condition essentielle de tout système de cryptographie, mais c’est un avantage trompeur et sur la réalisation pratique duquel on aurait tort de compter, à travers les mille péripéties d’une longue campagne.

Quant à la nécessité du secret, qui, à mes yeux, constitue le principal défaut de tous nos systèmes de cryptographie, je ferai observer qu’elle restreint en quelque sorte l’emploi de la correspondance chiffrée aux seuls commandants en chef. Et ici j’entends par secret, non la clef proprement dite, mais ce qui constitue la partie matérielle du système : tableaux, dictionnaires ou appareils mécaniques quelconques qui doivent en permettre l’application. En effet, il n’est pas nécessaire de se créer des fantômes imaginaires et de mettre en suspicion l’incorruptibilité des employés ou agents subalternes, pour comprendre que, si un système exigeant le secret se trouvait entre les mains d’un trop grand nombre d’individus, il pourrait être compromis à chaque engagement auquel l’un ou l’autre d’entre eux prendrait part. Rien qu’à ce point de vue il y aurait lieu de condamner l’emploi du dictionnaire chiffré, qui est en usage aujourd’hui dans l’armée.

On m’objectera peut-être qu’en admettant le deuxième desideratum, il n’est guère possible d’établir un système complètement indéchiffrable. Il faut s’entendre : je sais très bien que vouloir dans ces conditions trouver un système mathématiquement indéchiffrable est chose mathématiquement impossible ; mais j’affirme, et non sans de bonnes raisons, que, tout en réalisant les différents desiderata que j’ai énumérés plus haut, on peut parfaitement combiner des systèmes, sinon mathématiquement, du moins matériellement indéchiffrables.

Il paraît qu’il est sérieusement question, au ministère de la guerre, de remplacer le dictionnaire chiffré par quelque autre système plus pratique. Eh bien ! si l’Administration veut mettre à profit tous les services que peut rendre un système de correspondance cryptographique bien combiné, elle doit absolument renoncer aux méthodes secrètes, et établir en principe qu’elle n’acceptera qu’un procédé qui puisse être enseigné au grand jour dans nos écoles militaires, que nos élèves seront libres de communiquer à qui leur plaira, et que nos voisins pourront même copier et adopter, si cela leur convient le dirai plus : ce ne sera que lorsque nos officiers auront étudié les principes de la cryptographie et appris l’art de déchiffrer, qu’ils seront en état d’éviter les nombreuses bévues qui compromettent la clef des meilleurs chiffres, et auxquelles sont nécessairement exposés tous les profanes ; alors seulement cet article du règle ment du 19 novembre 1874, que j’ai mentionné plus haut, pourra recevoir une application pratique et réellement satisfaisante.

III. LES DIFFÉRENTES MÉTHODES DE CRYPTOGRAPHIE.

On peut rapporter les différents systèmes d’écriture secrète à trois méthodes principales :

1. La méthode qui se borne à une simple transposition des lettres du texte en clair ;

2. Celle qui fait reposer la combinaison du chiffre sur une interversion de l’ordre alphabétique des lettres ;

3. Celle qui représente les syllabes, les mots, ou même des phrases entières par des nombres ou des groupes de lettres [24].

A. Méthode par transposition.

Les systèmes qui reposent sur une transposition des lettres sont très anciens ; ils permettent des variations nombreuses et ont servi de base à quelques appareils mécaniques, tels que les grilles, qui jouissent encore aujourd’hui de la faveur du public [25].

Voici un exemple de transposition élémentaire : les lettres de la dépêche ont d’abord été transcrites dans leur ordre naturel sur un certain nombre de lignes d’un nombre déterminé de caractères, puis on les a recopiées dans un ordre convenu [26] ; c’est le nombre représentant la seconde disposition qui constitue la clef du chiffre [27].

Une attaque simulée aura lieu demain matin à quatre heures.

= u s u q t e e u a t a m l r u e u a i a e l e a n i e u m i a m d i h r t q n e t a u a u f d c s r e e b a e

Une fois que le déchiffreur se doute du procédé qui a été adopté, et c’est ce qu’il voit tout de suite à la lettre E, qui en ce cas revient le plus souvent, le déchiffrement n’est plus qu’une affaire de tâtonnement. Il suffit dé compter au préalable le nombre des lettres du cryptogramme et de les décomposer en deux facteurs (55 = 5 × 11) ; l’un représentera le nombre des lignes horizontales et l’autre celui des colonnes verticales. Rien que la présence d’un q ou d’un x, le premier étant toujours suivi et l’autre étant généralement précédé d’un u, trahit le secret de la clef.

A l’occasion des derniers procès intentés aux nihilistes, les journaux russes ont fait connaître le chiffre secret adopté par les accusés : c’est un système de transposition double ; les lettres, après avoir été une première fois transposées par colonnes verticales, le sont une seconde fois dans le sens des colonnes horizontales. Le même mot sert de clef pour les deux transpositions [28] ; à cet effet, on le transforme en formule numérique, en mettant à la place de chaque lettre un chiffre arabe, et en s’y prenant de telle façon que la valeur des chiffres corresponde au rang des lettres dans le classement alphabétique [29].

Voici le procédé appliqué au mot Schuvalow :

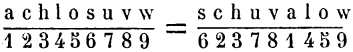
S’il s’agissait maintenant de transposer une phrase, comme celle-ci : Vous êtes invité à vous trouver ce soir, à onze heures précises, au local habituel de nos réunions, on procéderait d’abord comme dans le cas précédent, puis on reprendrait la même opération pour les lignes horizontales.

= s c i a u e s e l a v i v o n t e u v t r e r s o u c a c a b i o l h t n e l o s u d e r, etc.

Quelque compliquée que cette transposition puisse nous paraître, le déchiffrement d’un cryptogramme, écrit d’après ce système, ne saurait jamais présenter de difficultés insurmontables dans les langues où certaines lettres ne peuvent se présenter que dans des combinaisons déterminées, telles que le q ou le x français. Aussi les déchiffreurs russes paraissent-ils avoir mené leur besogne à bonne fin dans un temps relativement court.

Si l’on adopte un système plus compliqué, il cesse d’être pratique sans devenir pour cela beaucoup plus difficile à déchiffrer.

J’ai dit que la grille [30] repose sur le principe de la transposition des lettres ; c’est un procédé ingénieux, fort usité au siècle dernier, et que les perfectionnements récents introduits par le colonel autrichien Fleissner paraissent avoir rendu indéchiffrable [31].

La figure ci-après représente un ancien modèle : c’est une plaque métallique carrée, à 36 divisions, dont les 9 cases numérotées sont découpées à jour.

Supposons qu’on veuille écrire la phrase citée en premier lieu, moins les trois derniers mots : on place la plaque sur une feuille de papier, après y avoir préalablement tracé un carré de même dimension, et l’on écrit, aux endroits laissés ouverts, les 9 pre

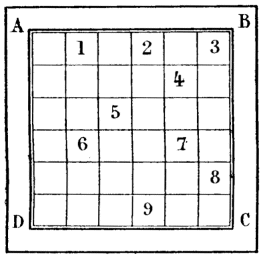
mières lettres de la dépêche ; on fait tourner ensuite l’instrument de droite à gauche, de manière que le côté BC prenne la place du côté AB ; on inscrit les 9 lettres qui suivent, et l’on retourne de nouveau la plaque pour continuer la même opération jusqu’à la 36^e lettre. On aura le cryptogramme suivant, où, pour plus de clarté, j’ai indiqué par des majuscules les initiales des mots :

= euunserimmaauatillateiameeaatquiduen.

La grille du colonel Fleissner (neue Patronen-Geheimschrift) est le fruit de longues et de patientes recherches, et peut être variée à l’infini ; mais, outre quelques inconvénients pratiques, elle ne peut, à mon sens, convenir aux usages de la guerre, par la raison qu’elle exige impérieusement le secret.

B. Méthode par interversion.

Dans les systèmes qui se rapportent à la méthode par interversion, il faut distinguer ceux à base invariable, c’est-à-dire où chaque lettre de l’alphabet est, dans le courant du même cryptogramme, représenté par le même caractère ou le même signe, et ceux à base variable, où l’on change d’alphabet à chaque mot ou à chaque lettre. On appelle communément les premiers systèmes à simple clef, et les seconds systèmes à double clef.

Les systèmes à simple clef ne présentent aucune sécurité ; les systèmes à double clef comportent seuls des combinaisons plus ou moins indéchiffrables.

1° Systèmes à simple clef.

Au point de vue de la forme, les systèmes à simple clef peuvent être variés à l’infini ; on peut non seulement combiner l’alphabet normal d’un nombre en quelque sorte incalculable de manières différentes, mais on peut encore remplacer les caractères alphabétiques par des nombres, des signes algébriques, astronomiques ou de fantaisie, ou encore par des groupes de lettres ou de chiffres, et même par des mots ou des phrases entières. Au fond cependant, et pour le déchiffreur, toutes ces combinaisons ne constituent qu’un seul et même système tombant sous l’application d’un même procédé de déchiffrement.

Le système à la fois le plus simple et le plus pratique est celui qui consiste à changer la valeur des lettres de l’alphabet d’après une clef convenue.

Nous avons vu, plus haut, comment on transforme un mot de clef en un nombre de clef; on peut adopter le même procédé pour établir l’ordre de succession des lettres du nouvel alphabet. Soit Champigny la clef ; la formule numérique y correspondant est 241685379. Si nous voulions ordonner l’alphabet cryptographique d’après ce nombre, nous obtiendrions :

Tournez les positions de l’ennemi donnerait avec cet alphabet le cryptogramme suivant :

VNSRQHY JHT LNTIVINQT FH JHQQHOI

Ce système est vieux de deux mille ans ; l’empereur Auguste s’en servait déjà pour écrire à ses enfants [32] ; et, au dire de Suétone et d’Aulu-Gelle, César lui-même n’avait rien su combiner de mieux, pour correspondre secrètement avec ses amis, qu’un alphabet où chaque lettre était avancée de quatre rangs [33]. Aussi se sert-on souvent du terme générique de méthode de Jules César pour désigner tout système qui repose sur une simple interversion des lettres de l’alphabet [34].

Il importe peu que les caractères cryptographiques soient des nombres, des signes de fantaisie ou les lettres ordinaires de l’alphabet.

La Bibliothèque nationale possède deux volumes de lettres chiffrées, trouvées à Offenbourg, par Moreau, dans les fourgons du général autrichien Klinglin, chargé du service de la correspondance secrète ; dans ces lettres, qui étaient très compromettantes pour le parti royaliste d’alors, chaque caractère du texte en clair est figuré par un nombre fixe, formé de deux chiffres arabes, tandis que la séparation des mots y est indiquée par un zéro. Il est probable que le général était plus fort en tactique militaire qu’en cryptographie, car il ignorait évidemment le principe si élémentaire que je viens de rappeler ; il a cru qu’il suffisait de découper arbitrairement quelques mots pour donner le change aux déchiffreurs.

Voici, au surplus, la première phrase d’une de ces lettres, datée du 31 décembre 1795 :

899952450 44520 455625365211250 si ce n’est la 3152891499 14 255452 44520 2311094259467524594995645 44118934 5294 445234114544520.

= Rien de nouveau, si ce n’est la certitude de la suspension d’armes demandée.

Je ne puis énumérer ici tous les systèmes à simple chef ; je dois me borner à citer parmi les anciens auteurs les noms de Tritheim [35], Porta [36], Blaise de Vigenère [37], Bacon [38], Hermann [39] et Mirabeau [40], qui ont imaginé des alphabets plus ou moins ingénieux, dont on peut trouver la description dans les traités spéciaux [41]. D’ailleurs, ces inventions ne peuvent avoir pour nous qu’un intérêt purement archéologique ; elles ne sont pas pratiques, et se déchiffrent toutes, celle de Hermann exceptée, avec une égale facilité.

2° Déchiffrement des systèmes à simple clef.

Quel que soit le système adopté, qu’il soit à base invariable ou à base variable, le déchiffrement d’un cryptogramme dont on n’a pas la clef comporte deux opérations bien distinctes : un calcul de probabilité et un travail de tâtonnement.

Le calcul de probabilité repose sur une particularité propre à toutes les langues, à savoir que certaines lettres reviennent plus souvent que d’autres, et que le rapport de ces répétitions est exprimé par une moyenne assez constante pour les 9 à 12 principales lettres de l’alphabet. Ainsi dans les langues française, anglaise et allemande, c’est la lettre E qui est le plus fréquemment répétée ; en espagnol c’est l’O, en russe l’A et en italien E et I ; en français, il y a en moyenne un E sur cinq lettres.

Ainsi, si on avait à cryptographier [42] une dépêche avec l’alphabet ci-dessous établi sur la clef Orléans, on saurait d’avance que c’est le chiffre A qui doit revenir le plus souvent.

Votre dépêche a été déchiffrée donnera, en effet, un cryptogramme où, sur 26 chiffres, le A est répété 9 fois :

ZSRPA BATACLA E ARA BACLMDDPNAA

Un calcul que j’ai fait sur quelques circulaires du Ministre de la guerre m’a donné une moyenne de 560 consonnes et 440 voyelles sur 1,000 lettres, soit :

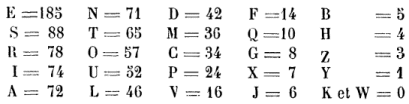
Lorsqu’on opère sur des dépêches d’une ou de deux lignes, on ne peut guère compter que sur l’E, et encore arrive-t-il quelquefois que le chiffre qui revient le plus souvent est un S, un R ou un I [43].

Outre la répétition des lettres prises isolément, il y a à noter leurs diverses combinaisons binaires ou ternaires, et une foule d’autres particularités, qu’il serait trop long d’énumérer ici.

Ainsi, pour les combinaisons binaires de l’E, on rencontre le plus souvent es et en ; viennent ensuite, et dans l’ordre de leur importance, se, te, et, de, me, el, em, le.

Je ne parle pas de la composition même des mots, car un système qui conserverait dans le texte chiffré la disposition extérieure des mots du texte en clair ne présenterait pas une ombre de sécurité.

En thèse générale, il suffit, dans le déchiffrement d’un cryptogramme, de connaître le caractère qui représente la lettre E, pour être assuré de trouver, soit par calcul, soit par tâtonnement, la signification de tous les autres. On pourrait même poser en principe que la valeur d’un chiffre se mesure aux garanties qu’il offre contre la découverte du signe correspondant à cette lettre [44].

Comme mon but n’est pas tant d’apprendre au lecteur à dé chiffrer que de lui indiquer la marche suivie par les déchiffreurs, je me contenterai de lui montrer par un exemple des plus élémentaires comment on procède pour le déchiffrement d’un texte dont on n’a pas la clef.

Soit le cryptogramme :

Le caractère qui se rencontre le plus souvent est b ; je dis qu’il doit correspondre à la lettre E, et je fais le raisonnement suivant :

N° 3. BOB : en fait de trigrammes commençant et finissant par un e, il n’y a que été.

N° 2. Z : la langue française n’a que deux monogrammes, a et y ; été ne peut être précédé de y, donc Z = a.

N° 7. JBJ : ce groupe ne peut être que ses ; c’est le seul tri gramme ayant un e au milieu, précédé et suivi de la même lettre.

N° 8. PBOOYBJ : nous connaissons déjà cinq lettres de ce groupe, .ett.es ; le seul mot qui réponde à cette disposition est lettres.

N° 1. SP : les seuls bigrammes qui peuvent aller avec a été sont ça, il, on ; or P est un l, donc SP = il.

N° 6. PSXB = lire.

N° 4. CSRRSQSPB : cinq chiffres nous sont déjà connus :  .i..i.ile.

La terminaison ile indique un adjectif ; en fait d’adjectifs en ile de neuf lettres ayant deux i dans le corps du mot, le dictionnaire des rimes ne donne que difficile.

N° 5. CB = de.

Nous avons donc : Il a été difficile de lire ses lettres.

Plus un cryptogramme est long, et plus il est facile de le déchiffrer ; en règle générale une ligne est suffisante.

Le général Lewal dit dans ses Etudes de guerre [45] qu’un chiffre à simple clef garantit suffisamment le secret pour les besoins ordinaires et « pour des affaires sans importance majeure. »

Je ne sais ce qu’il faut entendre par affaires sans importance majeure, mais le lecteur a pu s’assurer par le cryptogramme que je viens d’analyser qu’une dépêche écrite dans les conditions en question, lorsqu’elle a deux à trois lignes de longueur et qu’on n’a eu recours à aucun autre artifice, peut en quelque sorte être déchiffrée à vue.

Le chiffre à simple clef ne présente quelques légères garanties qu’aux trois conditions suivantes :

1° Que la séparation des mots ne soit pas indiquée dans le texte chiffré ;

2° Que les lettres doubles soient supprimées ;

3° Qu’on n’emploie ni majuscules, ni signes d’accentuation ou de ponctuation. Pour éviter les erreurs de transcription il est même indispensable de fractionner les cryptogrammes en groupes de quatre ou cinq chiffres [46]. Notre dernière dépêche devrait donc être cryptographiée comme suit il : il a été dificile de lire ses letres,

= SPZBO BCSRS QSPBC BPSXB JBJPB OXBJ

3° Systèmes à double clef.

Nous avons vu que les chiffres à double clef sont ceux où l’on change d’alphabet à chaque lettre.

Bien des combinaisons à base variable ont été imaginées, mais il n’y en a guère que trois ou quatre qui soient réellement pratiques et qui soient encore en honneur de nos jours ; quoique différentes pour la forme, elles sont identiques au fond, et reviennent au système exposé à la fin du xvi^e siècle par Blaise de Vigenère. Pendant près de trois siècles elles ont, servi de chiffre secret à la plupart des petites cours d’Allemagne et d’Italie, et aujourd’hui encore elles passent pour indéchiffrables aux yeux des personnes qui ne sont pas au courant des procédés de déchiffrement.

Comme toute méthode d’écriture cryptographique destinée aux besoins de l’armée doit pouvoir être appliquée à la télégraphie, nous n’avons à nous préoccuper que des systèmes qui sont uniquement basés sur l’emploi des lettres ou des chiffres arabes et cela avec exclusion de toute combinaison exigeant l’emploi simultané des deux [47].

a. Système de Porta.

L’invention du premier système littéral [48] à double clef remonte, comme je l’ai dit plus haut, au physicien Porta [49] ; quoique luimême ait été bien loin de sentir toute l’importance de l’introduction d’une clef proprement dite dans la méthode des écritures chiffrées, nous n’en devons pas moins le considérer comme le fondateur de la cryptographie.

Porta emploie onze alphabets différents, qu’il désigne, comme on le voit dans la figure ci-après, par les lettres AB, CC, etc., ou tout simplement par A, C, ou B, D.

Veut-on écrire avec l’un ou l’autre de ces alphabets, on choisit, pour représenter les lettres du texte en clair, celles qui, dans

le tableau, leur font face. Ainsi, Si l’on cryptographie avec l’alphabet D ou C, on représente a par z, et vice versâ z par a ; b par n et n par b, et ainsi de suite. Mais pour dérouter les calculs des investigateurs, Porta, en homme qui sait déchiffrer, recommande d’écrire chaque lettre avec un alphabet différent ; de plus, pour ne pas obliger les correspondants à prendre les onze alphabets à la suite, ce qui aurait bien vite trahi le secret, il propose de n’en adopter que quatre, cinq ou six, et de convenir d’un mot dont les différentes lettres indiqueront les alphabets qu’il faudra successivement choisir [50]. Ce mot constitue la clef du cryptogramme ; on l’écrit sous le texte à chiffrer, et on le répète le nombre de fois nécessaire.

Voici un exemple avec la clef roi :

= d h m a y z x i n t o n x a m v y y n p o y m n x

L’invention de Porta, avons-nous vu, ouvre, on quelque sorte, une nouvelle ère dans l’histoire de la cryptographie, mais elle présente deux grands inconvénients, qui l’ont fait abandonner depuis longtemps : d’abord le petit nombre de ses alphabets et ensuite la nécessité de représenter le même alphabet par deux lettres différentes. Par suite de cette dernière circonstance, un mot de quatre lettres, comme poli, donne une clef qui ne comporte en réalité que deux alphabets.

b. Chiffre carré ou tableau de Vigenère.

Le chiffre carré, aussi nommé le chiffre indéchiffrable ou chiffre par excellence, n’est autre chose que le système de Porta, simplifié par Blaise de Vigenère, qui l’a exposé, tel qu’il est encore en usage aujourd’hui, dans son Traité des Chiffres [51]. Le chiffre carré a joui d’un crédit extraordinaire auprès des chancelleries du xviii^e siècle, et, ce qui pourrait porter à croire qu’on n’a guère trouvé mieux depuis, c’est qu’on s’en est encore servi, après 1870, au ministère de la guerre.

Dlandol l’a fait connaître au public, à l’époque de la Révolution, dans un opuscule que j’ai déjà cité. Au chap. vi, il dit que « ce chiffre a été nommé le chiffre par excellence, parce qu’il réunit le plus grand nombre d’avantages que l’on puisse désirer pour une correspondance secrète. Il les réuniroit tous sans aucune exception », ajoute-t-il, « s’il n’étoit pas d’une exécution un peu lente ; mais il rachète bien cet inconvénient par la sûreté incroyable dont il est. Cette sûreté est telle que l’univers entier ne le connoitroit, si on ne savoit pas le mot de clef convenu entre les correspondants, on pourroit montrer sa lettre à tout le monde, sans que personne pût la lire. » Certes le citoyen Dlandol était meilleur patriote qu’habile déchiffreur !

La disposition du tableau de Vigenère diffère de celle du tableau de Porta, en ce que l’alphabet y est mis en nombre carré, et qu’on obtient ainsi autant d’alphabets différents qu’il y a de lettres dans l’alphabet [52].

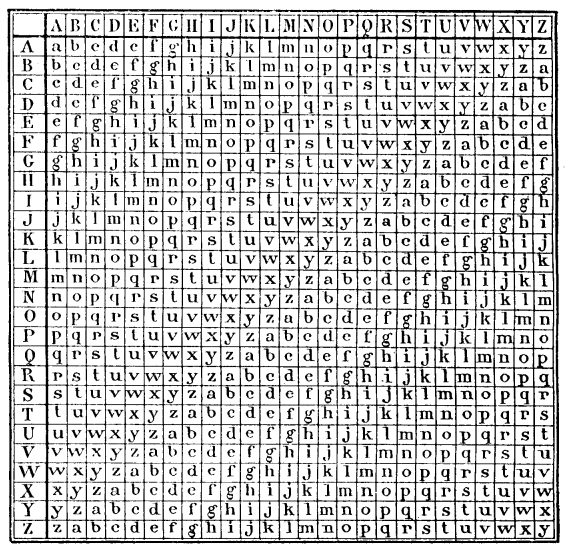
Quant au maniement de ce tableau, on procède comme pour le système de Porta ; il faut seulement remarquer que l’alphabet horizontal supérieur représente l’alphabet normal, et que les 26 autres qui suivent sont les alphabets cryptographiques.

Soit à cryptographier Détruisez le tunnel avec les trois alphabets correspondant au mot BAC ; on aura :

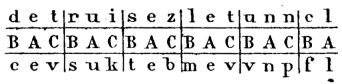
= e e v s u k t e b m e v v n p f l

Rien n’est plus facile que de lire un cryptogramme écrit dans ces conditions, lorsqu’on en connaît la clef : on transcrit le texte chiffré par tranches égales au nombre des alphabets choisis, on écrit en-dessous la clef, et l’on fait l’inverse de la première opération.

Soit donné à déchiffrer e y f d a o l r a k h h g m h n c f m k. Tunis étant la clef, on trouvera :

= Les vivres sont épuisés.

Ainsi que nous le verrons plus loin, les dépêches écrites avec le tableau de Vigenère se déchiffrent très facilement ; ce n’est que dans des cas exceptionnels que le système peut présenter quelque sécurité.

c. Système de Saint-Cyr.

Ce système, qui est en usage depuis longtemps, n’est autre chose qu’une forme déguisée du tableau de Vigenère ; faute d’une dénomination propre, je l’ai désigné sous le nom de l’école où il est enseigné et préconisé aujourd’hui.

En voici la description ; elle est prise dans le Cours d’Art militaire de l’année 1880-1881, tel qu’il a été autographié pour les élèves de la 1^re division [53] :

« L’instrument, y est-il dit, se compose d’un alphabet fixe, sous lequel glisse un double alphabet mobile ; deux bandes de papier quadrillé y suffisent [54].

On prend un mot quelconque de 3 à 5 lettres, pour former la clef [55]. Adoptons le mot BAC et prenons la dépêche suivante : Détruisez le tunnel.

« La clef ayant 3 lettres, on partage également la phrase à chiffrer en groupes de 3 lettres, comme il suit : dét — rui — sez — let — unn — el ; on chiffre d’abord les premières lettres de chaque groupe, puis les secondes, et enfin les troisièmes.

« Pour chiffrer les premières, on place la première lettre de la clef, B, prise sur l’alphabet mobile, sous la lettre A de l’alphabet fixe (voy. la fig. ci-dessus) ; et, prenant la première lettre de chacun des groupes de la dépêche sur l’alphabet supérieur, on écrit la lettre qui lui correspond sur l’alphabet inférieur.

« On passe ensuite aux deuxièmes lettres des groupes. Pour les chiffrer on place la deuxième lettre de la clef A sous la lettre A de l’alphabet fixe, et on opère comme nous venons de voir. On fait de même pour les troisièmes lettres. La dépêche se trouvera donc écrite comme suit :

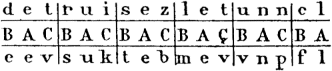
= e e v s u k t e b m e v v n p f l

« En admettant, ajoute le texte, que l’instrument soit perdu ou pris, il ne dit rien ; il faut connaître la clef. »

Il est facile de s’assurer que ce procédé n’est qu’un raccourci du précédent, en comparant dans les deux systèmes les trois alphabets qui correspondent à la clef BAC.

Chiffre carré.

Système de Saint-Cyr.

Comme ou obtient le même texte cryptographique avec les deux systèmes, le correspondant ou le déchiffreur n’ont même pas à se demander avec lequel des deux la dépêche a été écrite [56].

Le seul avantage que ce procédé présente sur le précédent, c’est que, en cas de perte, l’instrument peut être refait en deux ou trois minutes de temps. Au point de vue cryptographique, il n’acquiert une valeur réelle qu’à la condition d’intervertir l’ordre des lettres dans l’alphabet mobile.

Il est dit dans le Cours d’Art militaire qu’on pourrait établir l’instrument dans des conditions qui le rendraient plus portatif, en le formant au moyen de deux cercles concentriques, dont l’un serait mobile et tournerait autour de son axe ; ce serait ce dernier qui correspondrait au double alphabet.

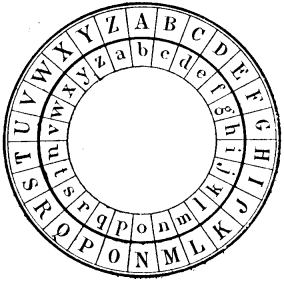
Cette disposition, qui est représentée dans la figure précédente, a été imaginée, dès 1563, par Porta [57], et a reçu depuis de nombreuses applications, telles que le cryptographe de Wheatstone et les boîtes à cadrans mobiles qu’on a vendues à l’époque de la guerre d’Italie. Tous ces appareils, dont quelques-uns sont présentés dans des ouvrages récents de télégraphie comme des inventions merveilleuses, ne sont en réalité autre chose qu’un simple tableau de Vigenère.

d. Système de Beaufort.

Une modification assez ingénieuse a été apportée au chiffre carré par l’amiral anglais Francis Beaufort (1857). Quoiqu’elle paraisse au premier abord n’affecter que le maniement du tableau, elle altère assez sensiblement le texte cryptographique pour lui donner aux yeux des non-initiés un véritable air d’indéchiffrabilité. Voici d’abord le tableau de Beaufort :

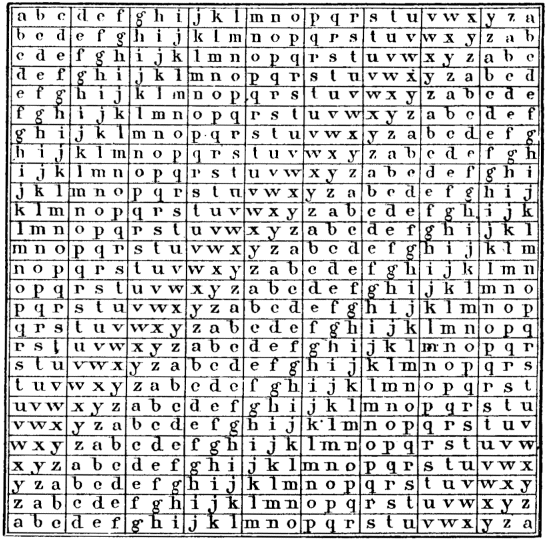
Emparez-vous des hauteurs, chiffré avec la clef BAC, donnera le cryptogramme suivant :

= x o n b j y c f o h i z x i v b g j x g l j.

Voyons maintenant comment on procède. Pointez la lettre e dans le premier alphabet horizontal, descendez en ligne droite jusqu’à la rencontre de b ; là, faites un demi-tour, soit à gauche, soit à droite ; avancez jusqu’à l’extrémité de la colonne, et la lettre x, que vous y rencontrez, est le signe cryptographique cherché ; et ainsi de suite avec les autres lettres.

Les déchiffreurs anglais, que le système de Beaufort a tant émerveillés, ne se doutaient certainement pas qu’on pût obtenir         le même résultat avec les systèmes de Vigenère ou de Saint-Cyr en retournant tout simplement l’alphabet normal [58].

Il est facile de s’en assurer par l’inspection des deux figures qui suivent :

Chiffre carré.

Système de Saint-Cyr.

Le résultat serait encore le même si, au lieu d’intervertir l’ordre des lettres dans l’alphabet normal, on mettait en nombre carré l’alphabet a z y x w v u t s r q p o n m l k j i h g f e d c b d’après le principe suivant :

e. Système de Gronsfeld.

Ce système ne diffère des deux précédents qu’en ce que le travail peut être fait de tête, au lieu d’exiger le concours d’un tableau ou d’un appareil quelconque.

Voici comment M. Bontemps, inspecteur des lignes télégraphiques, s’exprime à ce sujet [59] :

« Supposons qu’on ait choisi pour clef un nombre quelconque ; sous la phrase qu’on veut transmettre on l’écrit autant de fois qu’il peut y être contenu, en établissant la correspondance entre les lettres et les chiffres successifs. On prend pour lettre à envoyer celle qui est placée dans l’alphabet, à une distance de la véritable égale au chiffre posé en dessous, et l’on compose ainsi un grimoire dont il est impossible de découvrir la clef, « fût-on doué de la perspicacité que suppose à son héros Edgar « Poë dans le roman du Scarabée d’or, ou de l’intelligence des « agents employés à déchiffrer la correspondance de la duchesse « de Berry en 1832, d’après le récit qu’on trouve dans les mémoires de M. Gisquet. »

N’en déplaise à l’auteur que je viens de citer, le système du comte de Gronsfeld n’est pas beaucoup plus difficile à déchiffrer qu’un modeste chiffre à simple clef ; il n’est, d’ailleurs, qu’une forme déguisée du tableau de Vigenère [60].

Reprenons notre exemple, et soit encore une fois à chiffrer Détruisez le tunnel, avec la clef 102 : chaque lettre du texte en clair sera respectivement représentée par une autre, avancé un, un, zéro ou deux rangs :

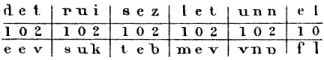
= e e v s u k t e b m e v v n p f l.

A la condition de prendre une clef composée exclusivement de nombres inférieurs à 10, ce système réalise parfaitement notre troisième desideratum, et offre même, si les nombres sont très bas, certaines commodités pratiques ; mais ces avantages perdent considérablement de leur valeur, en présence des facilités que cette disposition fournit aux investigations des déchiffreurs.

f. Système à clef variable.

Nous verrons plus loin que le déchiffrement des systèmes à double clef est principalement basé sur la connaissance du nombre de lettres composant la clef. On a songé à diverses combinaisons pour empêcher les déchiffreurs d’en faire le calcul ; une des mieux imaginées est due à un membre de la Commission de télégraphie militaire. Il propose d’arrêter, à des intervalles irréguliers, l’ordre de succession des alphabets, tel que l’indique la clef, pour revenir brusquement à la lettre initiale, ou alphabet premier. Ainsi, si la clef est Epaminondas, au lieu de la répéter régulièrement par séries de onze lettres, il la coupe arbitrairement, et il écrit :

epa + epaminondas epaminondas + epami + epaminon + etc.

Le point d’arrêt est indiqué par une des lettres de la clef, qu’on intercale aux endroits voulus dans le texte chiffré. En voici un exemple, où j’ai pris pour lettre d’arrêt la deuxième de la clef, soit P :

Pour éviter toute confusion dans la signification attribuée à la lettre d’arrêt, celle-ci est remplacée dans le texte cryptographique par un chiffre arabe correspondant à la place qu’elle-même occupe dans le mot de clef ; ainsi, dans l’exemple ci-dessus, où le P est la deuxième lettre de la clef, on la remplacera par un 2, à tous les endroits où elle ne doit pas jouer le rôle de lettre d’arrêt.

Avec le chiffre carré nous aurions le cryptogramme suivant :

r d u e P t 2 r f w a g P h t P q 2 a z.

Pour empêcher le déchiffreur de faire un tâtonnement sur les premières lettres de la dépêche, on la fait précéder de quelques nulles, en ayant soin d’indiquer par la lettre d’arrêt le point où commence le texte vrai. Notre cryptogramme pourrait donc s’écrire finalement :

x m o p r d u e p t 2 r f w a g p h t p q 2 a z.

Aug. Kerckhoffs,

Docteur ès lettres,

Professeur à l’École des hautes études commerciales et à l’École Arago.

(A continuer.)